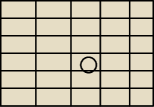
 (kratki wyszły mi troszkę nierówno, ale wszystkie powinny być takie same, kółko to moneta)
Na kartce narysowano linie pionowe i poziome tak, że odległości między sąsiednimi liniami są
równe "a" (patrz rysunek). Na kartkę rzucamy monetę o średnicy "a" tak, że środek monety leży
w jakiejś kratce. Jakie jest prawdopodobieństwo, że moneta zakryje punkt kratowy (wierzchołek
któregoś z kwadratów)?
(kratki wyszły mi troszkę nierówno, ale wszystkie powinny być takie same, kółko to moneta)
Na kartce narysowano linie pionowe i poziome tak, że odległości między sąsiednimi liniami są
równe "a" (patrz rysunek). Na kartkę rzucamy monetę o średnicy "a" tak, że środek monety leży
w jakiejś kratce. Jakie jest prawdopodobieństwo, że moneta zakryje punkt kratowy (wierzchołek
któregoś z kwadratów)?
 tylko z podręcznika, oznaczone jako trudne. Nie dopisałam tylko wskazówki,
która podpowiadała żeby rozważyć tylko jeden kwadrat i możliwości upadku monety w takim
wypadku.
tylko z podręcznika, oznaczone jako trudne. Nie dopisałam tylko wskazówki,
która podpowiadała żeby rozważyć tylko jeden kwadrat i możliwości upadku monety w takim
wypadku.
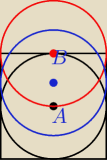 no to rozważam
tylko na odcinku AB mam nieskończenie wiele (naprawdę nieprzeliczalnie wiele) możliwych położeń
środka okręgu takiego aby żaden wierzchołek kwadratu nie został nakryty
nie mówiąc o innych możlowościach
no to rozważam
tylko na odcinku AB mam nieskończenie wiele (naprawdę nieprzeliczalnie wiele) możliwych położeń
środka okręgu takiego aby żaden wierzchołek kwadratu nie został nakryty
nie mówiąc o innych możlowościach
| π | ||
wyszło mi bodajże | , tylko nie wiem czy obliczyłam prawdopodobieństwo że zakryje jakiś | |
| 4 |
| 1 | ||
A=42π( | a)2 | |
| 2 |
| π | ||
P(A)= | ||
| 4 |
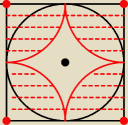 jeżeli chodzi o jeden kwadrat to:
potrzeba i wystarcza, aby środek koła (monety) leżał w odległości nie większej niż jego promień
r=a2 od jednego z wierzchołków kwadratu
to daje zakreskowany na czerwono obszar, czyli cztery ćwiartki koła o promieniu r czyli w sumie
całe koło
czyli dla jednego kwadratu jest tak jak liczyła Aska
jeżeli chodzi o jeden kwadrat to:
potrzeba i wystarcza, aby środek koła (monety) leżał w odległości nie większej niż jego promień
r=a2 od jednego z wierzchołków kwadratu
to daje zakreskowany na czerwono obszar, czyli cztery ćwiartki koła o promieniu r czyli w sumie
całe koło
czyli dla jednego kwadratu jest tak jak liczyła Aska
| π | ||||||||||||
P(A) = | = | ||||||||||||
| a2 | 4 |